¿Cómo se resuelve la ecuación matemática que divide a Twitter?: 8÷2(2+2)

ABC

07/10/2019 a las 17:17h.

Compartir

Esta funcionalidad es sólo para registrados

Iniciar sesión

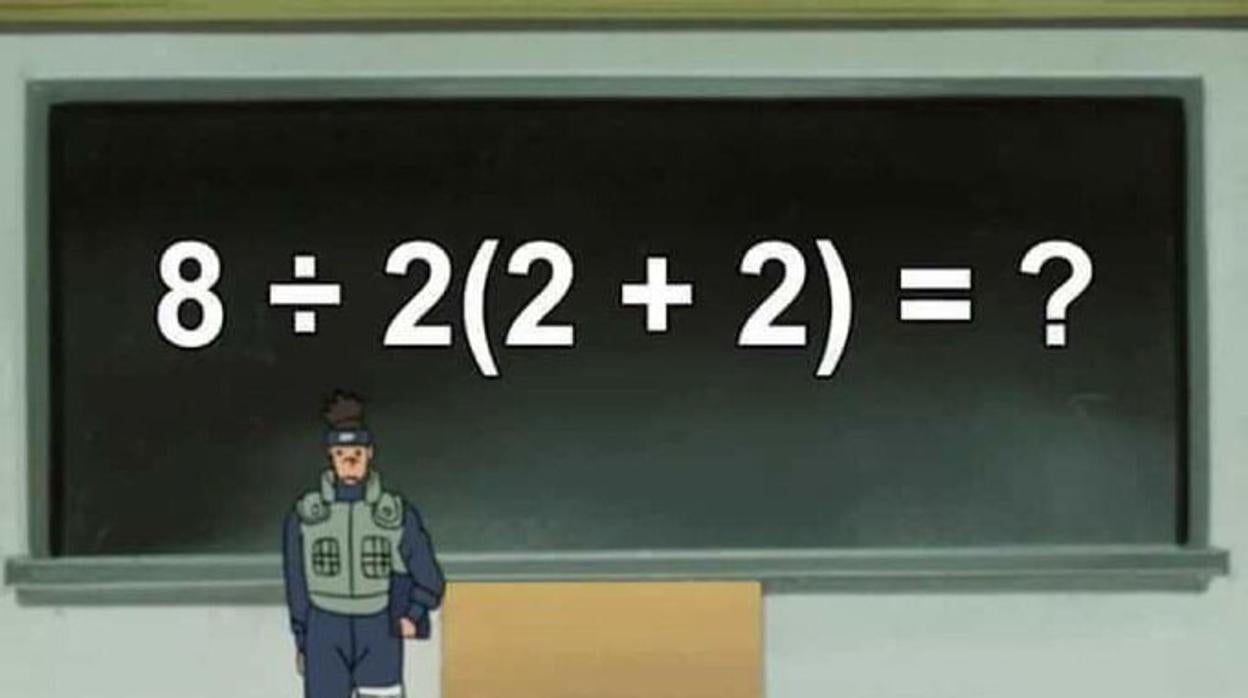
Desde comienzos de agosto, la operación « 8÷2(2+2) » ha dividido a cientos de usuarios tras viralizarse, sobre todo, a través de Twitter. ¿El motivo? La confusión generada respecto a cuál es la solución correcta .

Teniendo en cuenta que la forma en la que está escrita la ecuación es « ambigua » para muchos usuarios, existen dos posibles soluciones según el método matemático que se use para resolverla: «1» y «16» .

Tal es la confusión que hasta dos calculadoras serían capaces de dar ambos resultados , como mostró otra imagen viral.

Según un artículo de «The New York Times» , hay dos métodos para solucionar el problema: « PEMDAS » y « BODMAS », que se distinguen en función de la jerarquía de las operaciones cuando estas se muestran combinadas.

Así, «PEMDAS» vendrían a ser las siglas de Parentheses (Paréntesis), Exponents (Exponentes), Multiplication-Division (Multiplicación-División) y Addition-Subtraction (Suma y resta); mientras que «BODMAS» sería Brackets (Paréntesis), Orders (Exponentes), Division-Multiplication (División-Multiplicación) y Addition-Subtraction (Suma y resta).

Llegados a este punto, hay que tener en cuenta un error que el matemático Miguel Ángel Morales, autor de Gaussianos, trata de aclarar : por el orden de las letras, podría interpretarse el MD de PEMDAS «como que con este "método" la multiplicación tiene prioridad sobre la división, y el DM de BODMAS como que aquí es la división la que prioriza sobre la multiplicación. [...] Pues no, no es así la cosa: ni la multiplicación tiene prioridad sobre la división por el mero hecho de serlo, ni al contrario », explica.

En casos como este, en el que puede existir cierta confusión, lo más extendido (y correcto) es hacer aquellas cadenas de multiplicaciones y divisiones que no tengan paréntesis que indiquen prioridad de izquierda a derecha ; esto es:

La suma del paréntesis sería la operación de mayor prioridad: 2 + 2 = 4. Esto daría como siguiente expresión: 8 ÷ 2 x 4. Teniendo en cuenta lo anterior, tanto la «x» como la «÷» tendrían la misma prioridad, por lo que habría que hacer la operación de la izquierda, en este caso la división: 8 ÷ 2 = 4. Y en último lugar quedaría la multiplicación: 4 x 4 = 16 .

Ver comentarios (0)

Reportar un error