Matemáticas contra Daesh
Las Fuerzas de Seguridad y las agencias de Inteligencia utilizan modelos para combatir el terrorismo y la criminalidad organizada con resultados impactantes

¿Para qué sirven las matemáticas? La pregunta, realizada de forma recurrente por los alumnos a sus profesores durante décadas, siempre recibía, salvo pequeños matices, la misma respuesta: «Para todo», una contestación que naturalmente los escolares recibían con el escepticismo propio del desconocimiento. Pues bien, en ese «para todo» se incluye desde hace una década la lucha contra el terrorismo y el crimen organizado , de modo que esa disciplina se ha convertido en una herramienta eficaz en materia de seguridad.
Todas las organizaciones terroristas se enfrentan a un dilema: encontrar el equilibrio entre el necesario secretismo para ser opacos a los ojos de las Fuerzas de Seguridad y su capacidad operativa, para la que obviamente es necesario mantener contactos personales e intercambios de información o de cualquier otro tipo, como son los flujos económicos. La primera característica aporta seguridad, pero sin la segunda es imposible llevar a cabo una acción criminal en grupo.
Esta realidad es analizada con una herramienta matemática, el Social Network Analysis (SNA) -estudio de redes mediante la Teoría de Grafos- con la que se consigue caracterizar al grupo terrorista, entender su modo de actuar y articular la respuesta más eficaz para destruirlo.
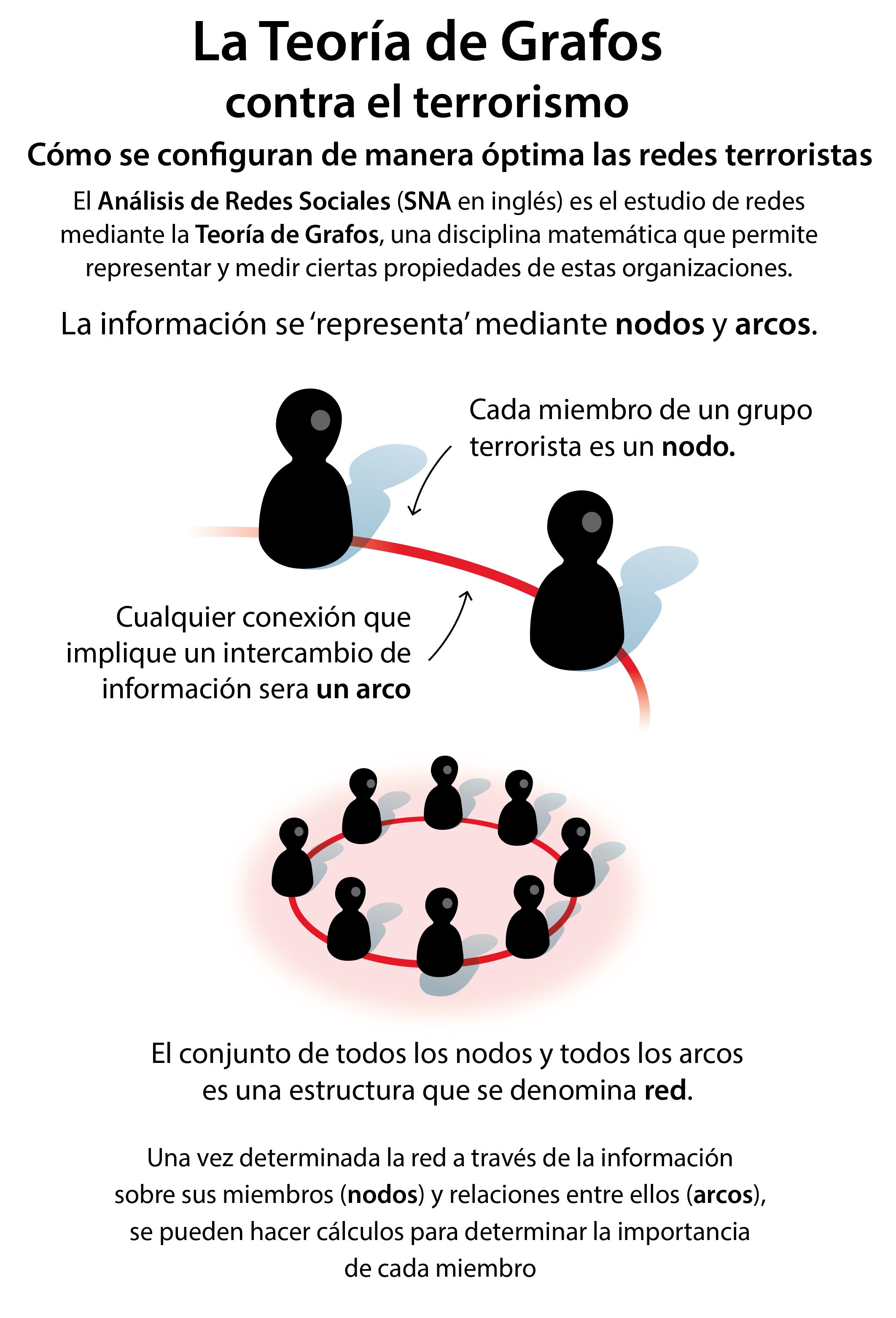
Carles Ortolà, ingeniero aeronáutico, profesor de la Universidad de Barcelona y experto en Inteligencia Estratégica y Seguridad explica a ABC que con la mencionada teoría «se consigue representar y medir las propiedades de las redes terroristas a través de los nodos -cada miembro de una de ellas- y arcos, que representan cualquier conexión que implique una relación, del tipo que sea, entre dos o más nodos».
El conjunto de todos los nodos y arcos conforma la estructura de la red. Ahora bien, no todos los nodos (personas) ni todos los arcos (conexiones entre ellas) son igual de importantes. Mejor aún; los primeros son más relevantes en función de la cantidad y calidad de los segundos, porque obviamente no tienen la misma importancia los contactos personales que la coincidencia espacial en un territorio más o menos amplio, pongamos por ejemplo. Es decir; la Teoría de Grafos permite calcular la centralidad de cada persona, o lo que es lo mismo, su importancia dentro de la organización terrorista.
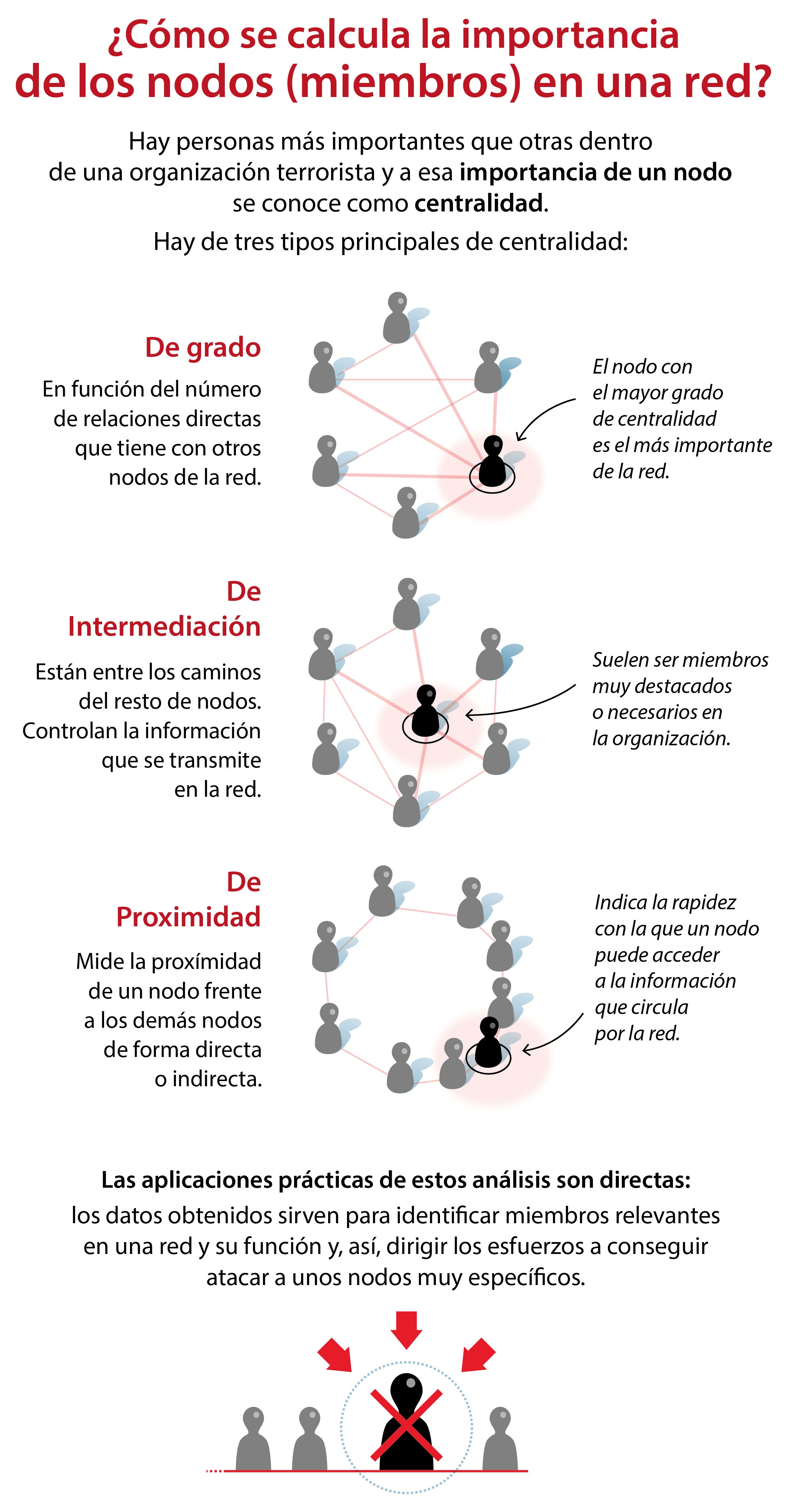
Con este modelo matemático se pueden medir distintas centralidades: de grado, según la cual una persona es más influyente en la célula cuantas más relaciones acumula; de proximidad, que calcula la capacidad que tiene alguien de llegar antes al resto de la red, de modo que se puede detectar a su líder logístico , y de intermediación, personas que unen partes de una red que de otro modo no se conocerían, y que son muy relevantes desde un punto de vista policial porque suponen en sí mismos una falla de seguridad de las organizaciones criminales. Un ejemplo es el miembro de la célula terrorista que tiene contactos con otra de venta de armas; sin él el grupo criminal no tendría acceso a ellas.
Naturalmente, explica Ortolà, «una correcta aplicación de la Teoría de Grafos permite planificar operaciones quirúrgicas en función de la estrategia policial que se diseñe. Y por supuesto, optimizar los resultados», ya que en un momento puede interesar atacar una parte de la red mientras se ve cómo reacciona otra ante esa acción policial.
Es una evidencia que las organizaciones criminales son más potentes cuanto más secretas, de modo que en la medida de lo posible evitan que sus miembros se conozcan y las comunicaciones se limitan al máximo. «La clave para los grupos es tener solo las conexiones suficientes para poder ejecutar una acción con eficacia», resume el experto.
Para las Fuerzas de Seguridad y las agencias de Inteligencia es clave medir esa eficacia, cómo de óptimas son las células. Ello depende de dos variables: el secretismo (S) y el flujo de información (I). Si el primero alcanza el máximo se le da un valor de 1, pero en ese caso el flujo de información sería inexistente . De la misma forma, si el segundo tiene un valor de 1, la organización estaría completamente expuesta. Cuando se aplica la fórmula matemática correspondiente, el parámetro «Q» es el que mide la eficiencia de la organización terrorista, lo que sirve para saber si es muy activa, tiene futuro o está condenada al fracaso.
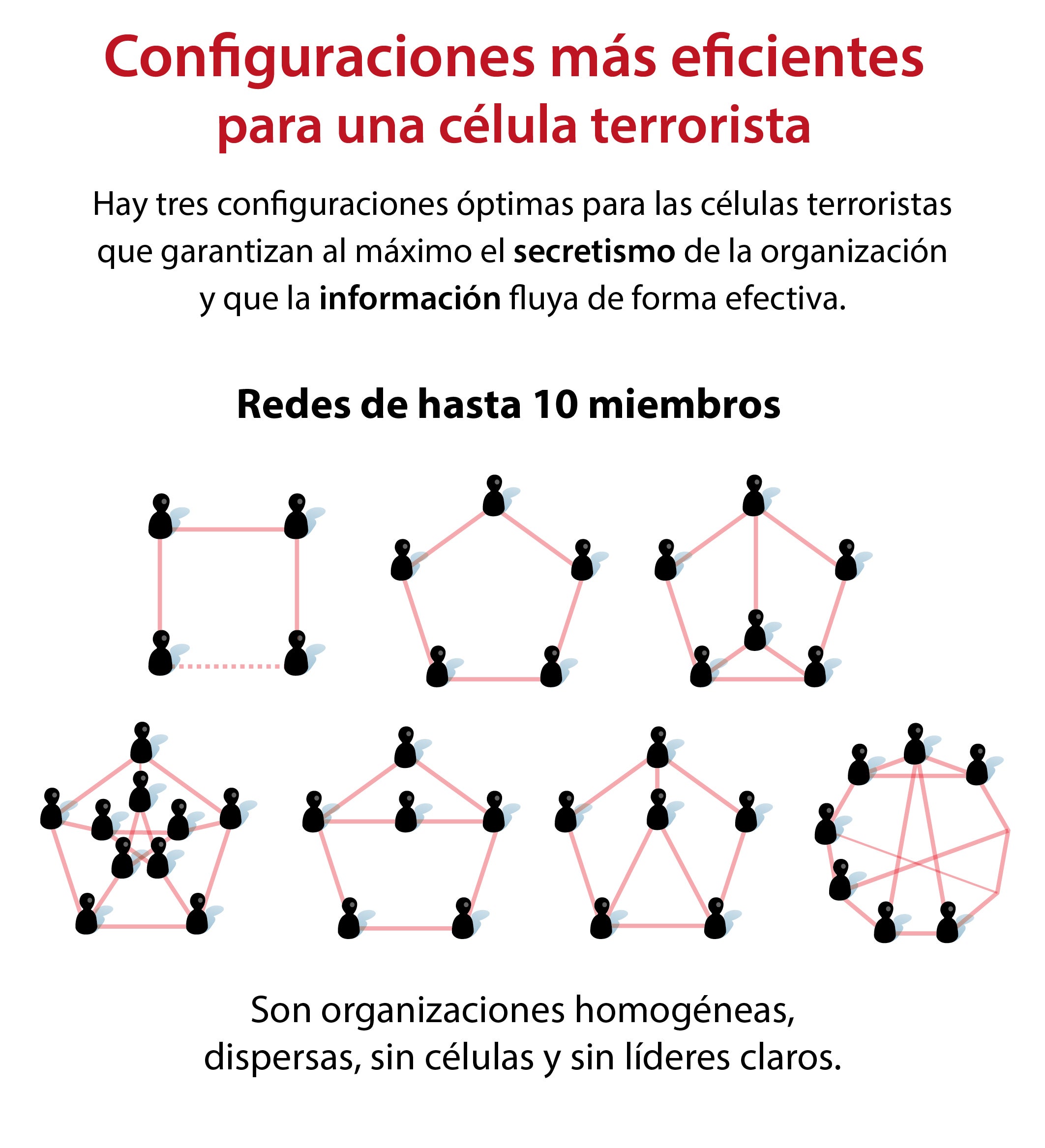
Por supuesto, en la eficiencia también influye la organización interna óptima de cada tipo grupo. «No es lo mismo -explica Ortolà- una célula de seis personas que otra de más de medio centenar. Las matemáticas nos dicen cuál es la mejor posible. Cada una debe de tener una estructura diferente para alcanzar su mayor grado de eficacia».
La configuración más eficaz para las células de hasta diez personas (nodos) son diferentes en función de si su número de miembros es de siete o más (ver ilustración). Los nodos están conectados estrictamente lo necesario para garantizar al máximo el secretismo y al mismo tiempo asegurarse de que la información pueda influir de forma efectiva.
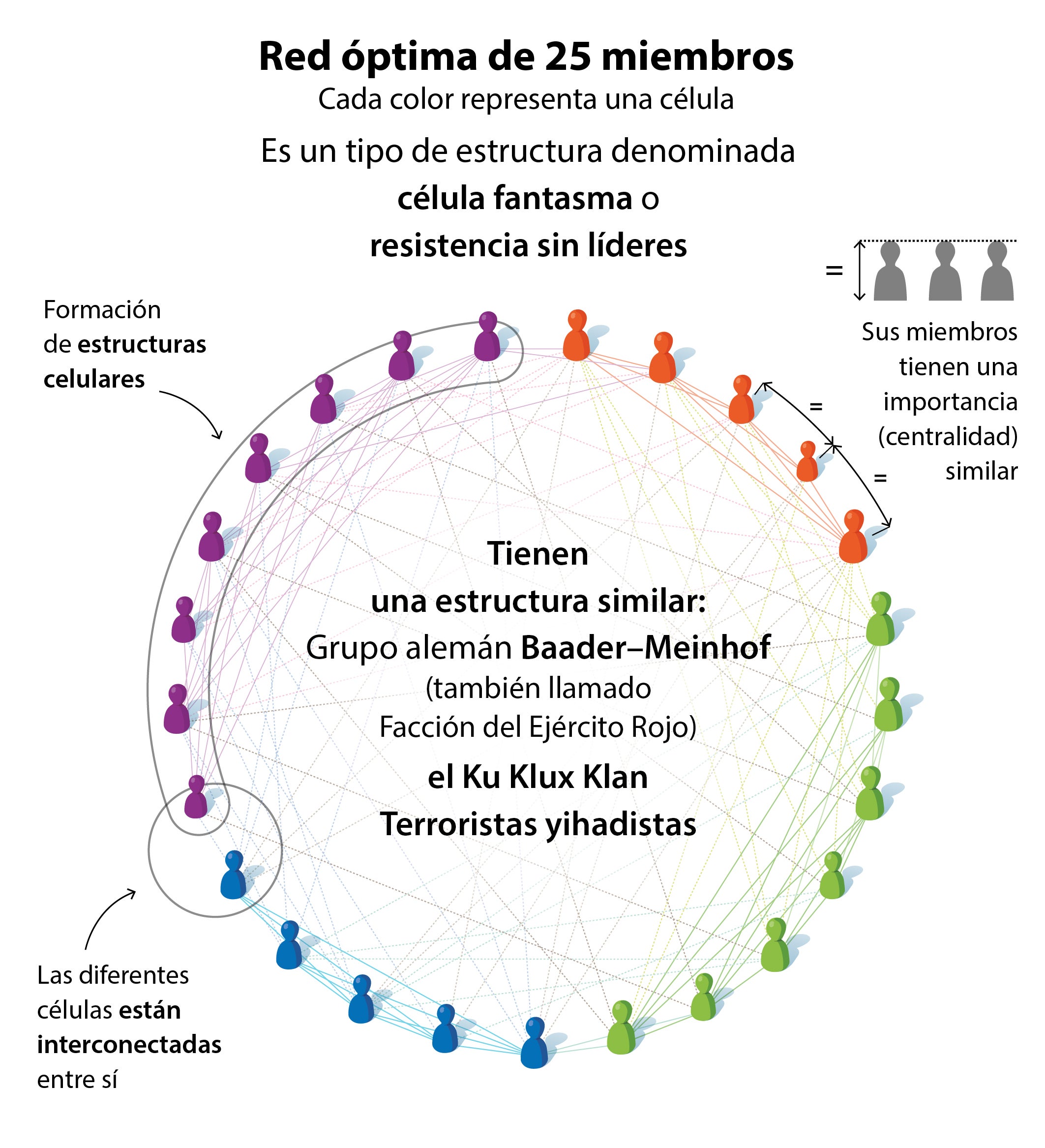
Cuando la red tiene hasta 25 miembros las matemáticas concluyen que su configuración óptima es horizontal, sin líderes, de modo que cada miembro se conoce pero cada uno actúa por su cuenta. No hay subgrupos más o menos autónomos; por tanto, son horizontales y dispersas.
A partir de los 25 miembros, el algoritmo indica que su organización más eficaz es mediante células interconectadas entre sí, pero sin líderes jerárquicos definidos. Esta estructura se pudo observar en la Baader-Meinhof alemana, el Ku Klux Klan o los grupos yihadistas , donde hay células aparentemente sin jerarquía, de menor tamaño, atomizadas y sin líderes claros, perpetrando sus ataques más por afinidad ideológica que por órdenes directas de un jefe. Es decir, un escenario de casi guerra de guerrillas.
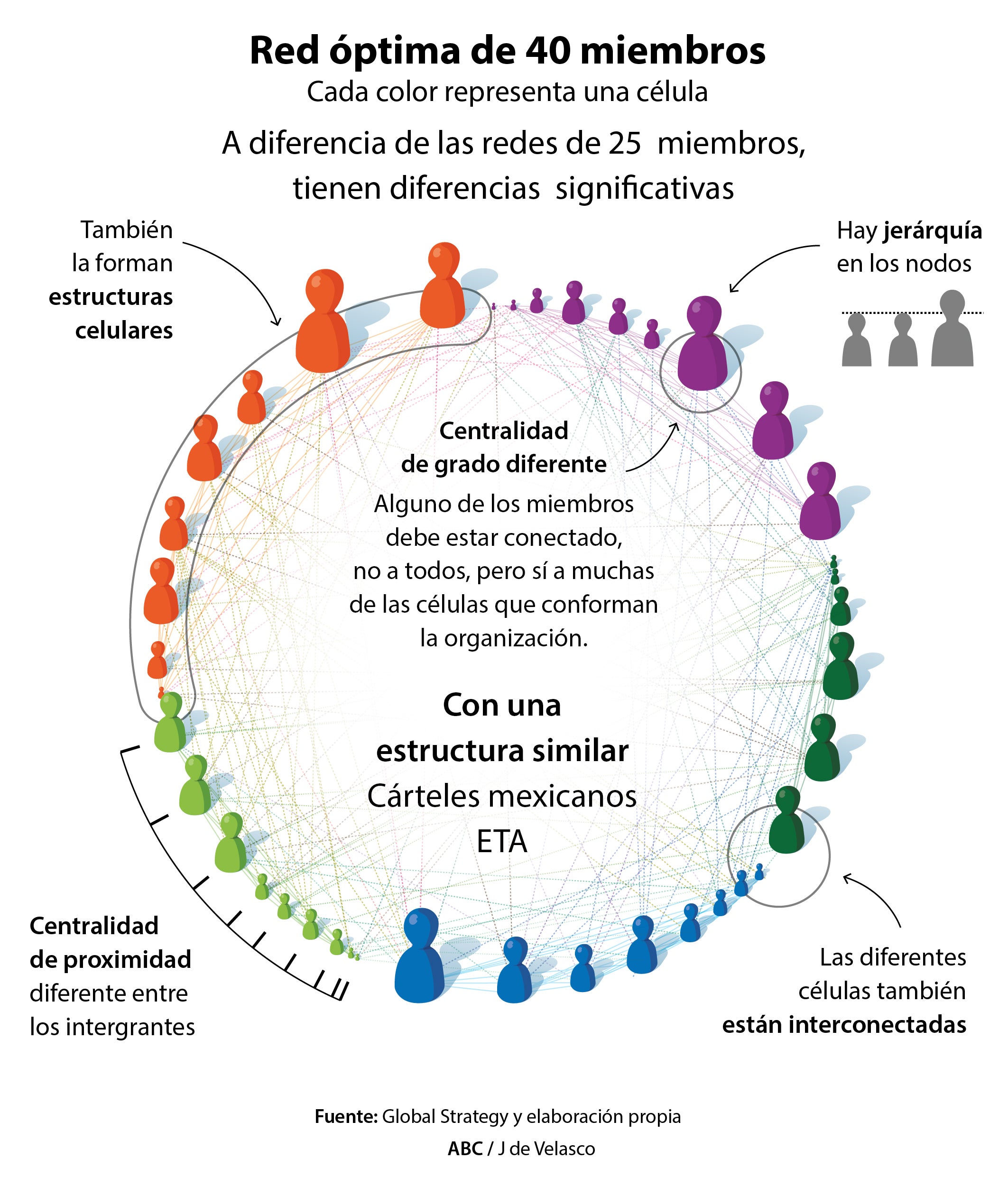
Finalmente, cuando la organización terrorista supera los 40 miembros se siguen manteniendo las estructuras celulares, pero ya aprecian nodos (individuos) con centralidades más significativas (con más conexiones que el resto). «Las redes óptimas de estas características -precisa Ortoà- necesitan de una estructura jerárquica y de alguna persona conectada no a todas, pero sí a muchas de las células que conforman la red. Cada una de ellas tiene un jefe, que se relaciona con otros de otras, de más o menos relevancia». Nuestro ejemplo doméstico más evidente es el de la banda terrorista ETA.
En general, a medida que aumenta el número de miembros de estas tramas los valores conjuntos comienzan a diluirse. Un ejemplo muy evidente es la evolución de las redes de la droga en México, donde históricamente se ha comprobado que los grupos solo han conseguido una estabilidad cuando han existido líderes claros que, aún otorgando cierta independencia a las células han servido como aglutinante, aunque solo sea ideológico, místico o de respeto entre todas ellas.
«Los modelos matemáticos no solo predicen cómo son las formas más eficaces de cada organización, sino que la realidad corrobora que están en lo cierto», explica Carles Ortolà. «Es absolutamente necesario potenciar la transferencia de conocimientos del mundo científico al de la seguridad. En Estados Unidos se hace ya con éxito, pero en España es aún incipiente». En nuestro país es el Ejército el que más ha avanzado en este campo, pero queda mucho por progresar.
Noticias relacionadas