Explican con matemáticas el extraño movimiento que ni siquiera Albert Einstein llegó a comprender
El físico alemán describió los movimientos aleatorios de partículas en un fluido y ahora han descrito lo que ocurre cuando en ese fluido hay nadadores

La importancia científica de Albert Einstein va mucho más allá de la Relatividad o de su predicción acerca de la existencia de las ondas gravitacionales. En el año milagroso de 1905 explicó el efecto fotoeléctrico (lo que le valió el Nobel y permitió arrancar a la teoría cuántica) y estableció la equivalencia entre masa y energía, expresada en su fórmula más famosa (E=mc^2). Además, creó una teoría matemática para describir el movimiento browniano : un sorprendente fenómeno por el cual pequeñas partículas suspendidas en un fluido se mueven aleatoriamente, dando pequeños tumbos, como si estuvieran animadas (esto puede verse fácilmente al microscopio y se puede decir que es similar a los movimientos de cada insecto dentro de una nube de mosquitos).
Noticias relacionadas
La historia del movimiento browniano se remonta a 1827, fecha en la que el escocés Robert Brown describió un movimiento aleatorio de gránulos de polen (de la especie Clarkia pulchella ) en el agua. En un principio pensó que era la vida la que les impulsaba, pero luego observó que hasta las partículas inertes se movían vivamente. Medio siglo después se comenzó a hablar de que en líquidos y gases había moléculas moviéndose constantemente (y que más lo hacían cuanto mayor fuera la temperatura) y los físicos James Clerk Maxwell, Ludwig Boltzmann y Rudolf Clausius fueron desarrollando la teoría cinética de los gases . Teniendo en cuenta todo esto, ya en 1905 Einstein corroboró cuantitativamente la teoría del movimiento browniano (a la vez que el físico polaco Marian Smoluchowski) con un modelo matemático. Todo esto fue allanando el camino para el desarrollo de la teoría atómica.
Pero hubo algo que ni Einstein (ni Smoluchowski) pudieron explicar matemáticamente: los movimientos que experimentan las partículas inertes en el entorno real , donde hay seres que nadan por sus propios medios y rompen el equilibrio ideal que asumen los cálculos, generando bucles y complejas trayectorias que no pueden ser descritas por los ecuaciones de los movimientos brownianos. Ahora, por primera vez, un grupo de investigadores ha presentado una nueva teoría capaz de explicar los movimientos de las partículas incluso en esos entornos. Creen que su modelo podría servir para explicar los movimientos de microorganismos en el agua o incluso predecir fenómenos en mercados financieros o en epidemias. Sus conclusiones se han publicado en la revista « Nature ».
«Hemos solucionado el antiguo problema de cómo una partícula se difunde en un medio activo donde hay nadadores , lo que tiene importantes diferencias en comparación con el movimiento browniano», ha explicado Adrian Baule , director de la investigación y profesor en la Universidad Queen Mary de Londres, a ABC.
Los movimientos de las partículas inertes que están en un fluido donde hay nadadores sencillamente no se rigen por los movimientos brownianos , donde las partículas dan tumbos siguiendo trayectorias rectas muy cortas . Pero en este caso, las trayectorias son más largas. De hecho, ahora los científicos han descubierto y demostrado que el movimiento de las partículas en esas condiciones sigue un comportamiento que fue descrito por el matemático Paul Lévy: el llamado « vuelo de Lévy ».
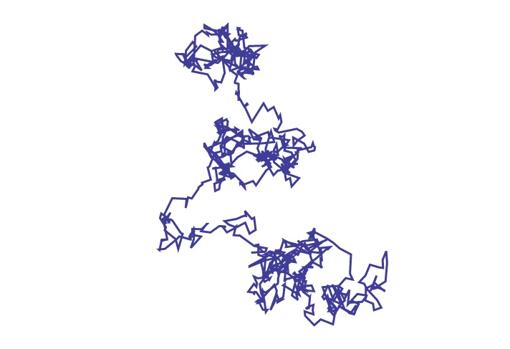
«El vuelo de Lévy es un tipo de "caminar aleatorio", donde cada paso -adoptado por una partícula inerte- puede tener una longitud muy larga», ha explicado Baule, desde luego más larga que las trayectorias de las partículas determinadas por movimientos brownianos. «Estos vuelos de Lévy son invariantes en relación con la escala y auto-similares -lo que quiere decir que el todo es idéntico a una parte de sí mismo, de forma similar a los patrones de un brócoli romanesco- lo que son propiedades de los fractales . Esto quiere decir que si amplias el zoom de una trayectoria, a pequeña escala tiene el mismo aspecto que a gran escala», ha aclarado el profesor.
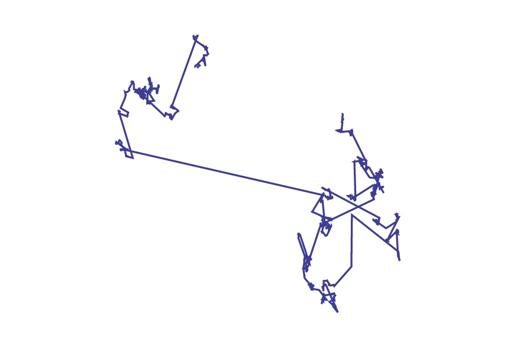
En este caso, por primera vez, los investigadores han observado que los movimientos de las partículas en un fluido donde hay nadadores se ajustan a este peculiar patrón. Esto significa que existen unas interacciones físicas que lo hacen posible y que, quizás, «los organismos nadadores puedan aprovecharse de esta propiedad para conseguir comida», ha sugerido Baule. De hecho, los autores de este trabajo han propuesto que su modelo matemático podría servir para hacer predicciones sobre comportamientos adoptados por algas o bacterias nadadoras.
Pero no solo eso. El patrón de los «vuelos de Lévy» aparece también en sistemas ecológicos, terremotos o en las rutas de grandes animales, como los tiburones, se cree que porque permite optimizar el forrajeo o búsqueda de comida.
Gobernado por leyes físicas
La diferencia, y lo que hace relevante a este trabajo, es que los autores han podido asociar el patrón de Lévy unas leyes físicas que surgen en un sistema de múltiples partículas: «Nuestro trabajo es el primero donde el vuelo de Lévy realmente surge de un sistema de múltiples partículas donde las interacciones están modeladas por leyes físicas ; en este caso, interacciones hidrodinámicas». Y esto, según los autores del trabajo, es muy sorprendente.
Estudiando estas leyes físicas, han descubierto que la densidad de nadadores y de partículas modulan «el aspecto» de los vuelos de Lévy. De hecho, la concentración de partículas, que podrían ser perfectamente de comida o de un compuesto contaminante a degradar, llevaría a que los microorganismos nadadores se moviesen más o menos para optimizar su búsqueda.
Útil para comprender mercados y epidemias
En opinión de Adrian Baule esta investigación revela cómo lo aleatorio surge de un medio en desequilibrio , lo que es importante para comprender multitud de sistemas físicos, biológicos o incluso humanos, como lo son los mercados financieros: «Los vuelos de Lévy se pueden ver en los mercados, donde los eventos extremos son más probables que en los movimientos brownianos convencionales. Por eso, creo que nuestro trabajo sirve para hacer modelos con los que describir estos sistemas y, quizás, diseñar nuevas regulaciones».
De hecho, Kiyoshi Kanazawa , primer autor del estudio e investigador en la Universidad de Tsukuba (Japón), ya está trabajando en esta dirección: «Todavía es una idea aproximada, pero estoy realmente interesado en explorarla», ha explicado a este periódico.
Además, Baule ha explicado que están interesados en explorar estos fenómenos para imaginar dispositivos artificiales, como motores a pequeña escala , o incluso para aplicarlos a la epidemiología.
