La crisis actual, explicada por la Física
Cuatro científicos interpretan la situación económica y la posible recuperación a través de las leyes de Newton
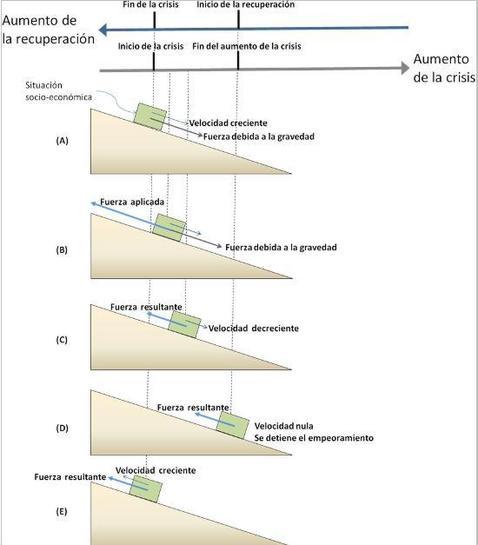
Vamos a intentar dar una interpretación mecanicista de la relación entre crisis y su posible recuperación, mediante la analogía de un cuerpo, de masa m, desplazándose sobre un plano inclinado sin rozamiento. La posición del cuerpo en cada momento la asociaremos a un estado de la situación socio-económica. Representaremos cinco fases del movimiento del cuerpo que denotaremos mediante Fases (A), (B), (C), (D) y (E) y que se indican en la Figura 1
En la Fase (A) se inicia la crisis, el bloque comienza a moverse hacia la parte inferior del plano, aumentando la crisis al mismo ritmo que aumenta su velocidad y el paro al mismo ritmo en que aumenta la distancia del cuerpo a su posición inicial. La fuerza que hace moverse al cuerpo es la componente tangencial de su peso. La componente normal, que no se representa en la figura, queda compensada por la fuerza normal, de igual magnitud y dirección pero de sentido contrario, que el plano ejerce sobre el cuerpo. Tanto las fuerzas tangencial y normal tienen su origen en la gravedad y son las componentes del peso, es decir, de la fuerza que la Tierra ejerce sobre el cuerpo, y ambas son constantes.
Estas dos fuerzas son intrínsecas al peso del cuerpo y existen independientemente de cualquier posible acción del observador. Por lo tanto se mantienen en todas las situaciones indicadas en la Figura 1. Siempre que sobre un cuerpo de masa m actúa una fuerza, F (que es una magnitud vectorial), aquél está animado de una aceleración, a (que es también una magnitud vectorial) que tiene siempre la misma dirección y sentido que la fuerza. La fuerza, la aceleración y la masa del cuerpo están relacionadas mediante la segunda ley de Newton, F = ma. Por lo tanto la aceleración es constante si la fuerza es constante. Esta afirmación es independiente de que la fuerza, F, sea la única que actúa sobre el cuerpo o sea la fuerza resultante de un conjunto de fuerzas que actúan sobre el cuerpo.
En nuestro caso, sobre el cuerpo actúan dos fuerzas: el peso y la fuerza perpendicular, normal, al plano que éste hace sobre el cuerpo. La resultante de estas dos fuerzas es precisamente la fuerza tangencial, paralela al plano, la cual es la responsable del desplazamiento del cuerpo hacia abajo con una aceleración constante. Debido a la aceleración asociada a esta fuerza, la velocidad del cuerpo en su movimiento hacia la base del plano inclinado es cada vez mayor. En la Figura 2 representamos, con detalle, todas las fuerzas que actúan sobre el cuerpo en esta primera Fase (A)
En la Fase (B)se aplica una fuerza adicional sobre el cuerpo de sentido contrario (hacia arriba del plano inclinado) y mayor que la fuerza tangencial debida a la gravedad. ¿Quién hace esta fuerza? La respuesta es sencilla, quien intente revertir la situación, para lo cual se aplican reformas y medidas varias.
En la Fase (C) vemos que la fuerza resultante sobre el cuerpo es de sentido contrario al de su velocidad de caída por el plano. La aceleración del cuerpo, ahora, tiene sentido contrario a la que tenía en la Fase (A), por lo que la velocidad del cuerpo es cada vez menor. Obsérvese que en esta situación la velocidad y la aceleración tienen sentido contrario. Este hecho no ocurre con la fuerza y la aceleración, que siempre son vectores de la misma dirección y sentido, la aceleración (y por lo tanto la fuerza) y la velocidad no tienen por qué tener la misma dirección y sentido. La velocidad en esta fase sigue teniendo el mismo sentido que en (A) y (B) pero ahora es cada vez menor, el bloque continúa cayendo; pero se va frenando. Sigue aumentando la crisis, hay síntomas de mejora; pero todavía no son apreciables en la economía.

En la Fase (D) la velocidad se anula, es el final del empeoramiento de la crisis y el comienzo de la recuperación. A partir de la Fase (D) la velocidad cambia de sentido con respecto a las Fases (A), (B) y (C), y va aumentando, la recuperación es cada vez mayor, ya es apreciable. Por último, en la Fase (E) se representa el cuerpo en la misma posición que en (A); pero ahora está subiendo por el plano en lugar de deslizarse por él.
Obsérvese que si comparamos (B) y (D), a pesar de la fuerza aplicada, de las medidas económicas y de empleo tomadas, la situación sigue evolucionando hacia la parte inferior del plano, pero cada vez con menor velocidad, hasta que a partir de (D) comienza el cuerpo a ascender por el plano inclinado, comienza la recuperación.
En la analogía utilizada el aumento de la distancia recorrida por el cuerpo mientras baja por el plano sería equivalente al aumento del paro, en contrapartida la recorrida mientras el cuerpo sube por el plano sería equivalente a la disminución del paro.
Desde luego, si la fuerza aplicada es menor, en valor absoluto, que la debida a la gravedad, la crisis aumentaría continuamente, el cuerpo estaría cada vez más abajo y acabaría estrellándose contra el suelo en la parte baja del plano, sería la quiebra total, como se indica en la Figura 3.

Pero queremos presentar una visión optimista y nos resistimos a considerar esta inquietante situación. Se ha prescindido del rozamiento entre el cuerpo y el plano por no romper la evolución ideal que hemos planteado y que no sabemos si se acercará más o menos a la evolución real. Creemos que actualmente estamos en una situación intermedia entre (C) y (D), aunque otros ya declaran que estamos subiendo por el plano inclinado. Esperemos como dijo Pascal que “no es cierto que todo sea incierto” y podamos ver cómo salimos de esta crisis, para lo cual la fuerza aplicada debe surtir sus efectos.
Noticias relacionadas
- Diez curiosidades meteorológicas sobre el invierno que la física puede explicar
- Diez descubrimientos de premio Nobel explicados en un esquema
- Los diez grandes avances de la Física en 2014
- Los inventores de las bombillas LED de bajo consumo, Nobel de Física 2014
- John Ellis: «Hay aún muchos misterios ligados al bosón de Higgs»